2023学年中考数学压轴题冲刺提升专题01动点与函数图象含解析.docxVIP免费

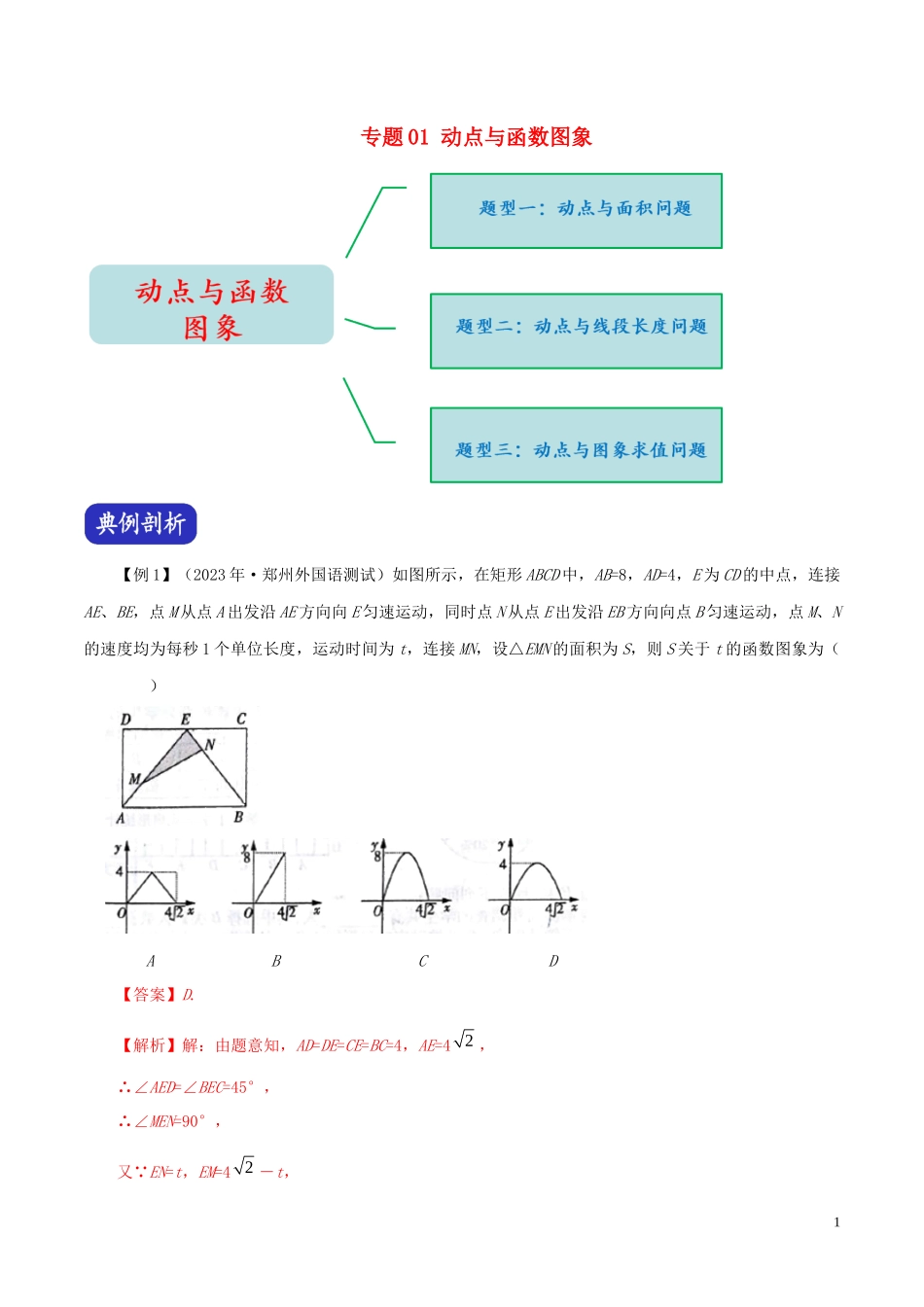
专题01动点与函数图象【例1】（2023年·郑州外国语测试）如图所示，在矩形ABCD中，AB=8，AD=4，E为CD的中点，连接AE、BE，点M从点A出发沿AE方向向E匀速运动，同时点N从点E出发沿EB方向向点B匀速运动，点M、N的速度均为每秒1个单位长度，运动时间为t，连接MN，设△EMN的面积为S，则S关于t的函数图象为（）ABCD【答案】D.【解析】解：由题意知，AD=DE=CE=BC=4，AE=4，∴∠AED=∠BEC=45°，∴∠MEN=90°，又 EN=t，EM=4－t，221∴S===，（0≤t≤4）图象为抛物线，开口朝下，当x=2时，S取最大值4，故答案为D.【变式1-1】（2023年·洛阳二模）如图，点P是边长为2cm的正方形ABCD的边上一动点，O是对角线的交点，当点P由A→D→C运动时，设DP=xcm，则△POD的面积y（cm2）随x（cm）变化的关系图象为（）ABCD【答案】B.【解...