2023学年中考数学冲刺专题卷专题12压轴题含解析.docVIP免费

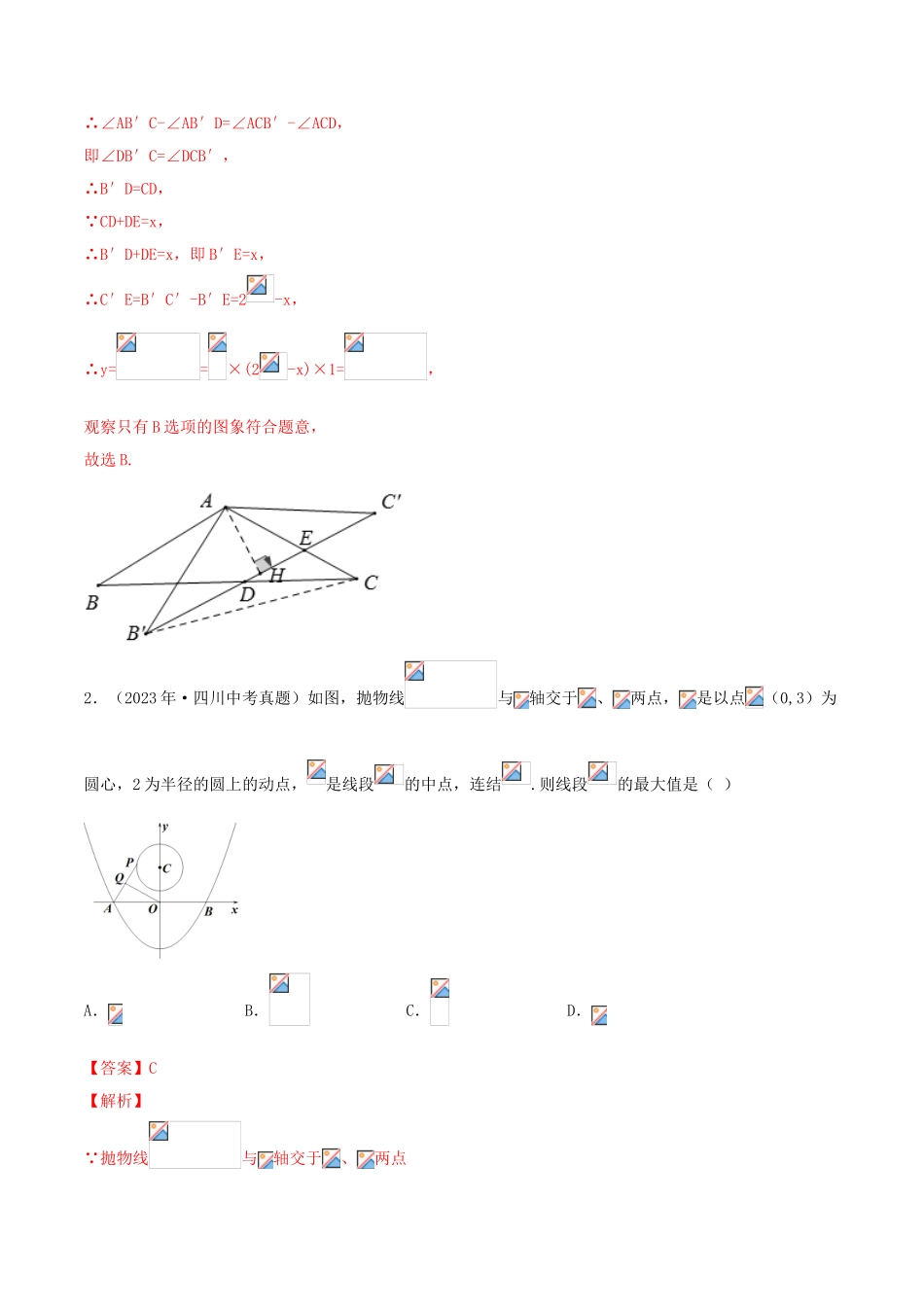
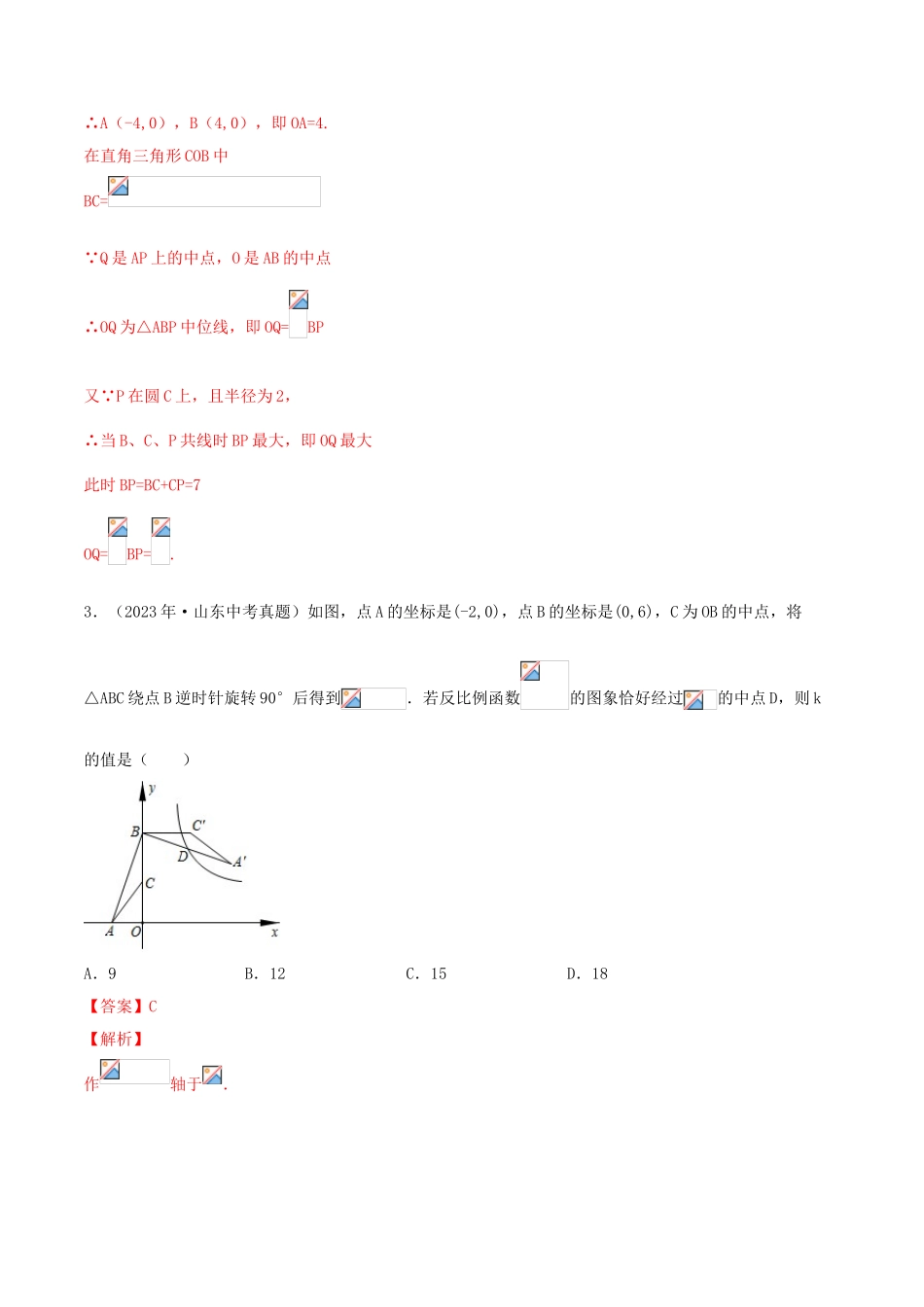
2023年年中考数学冲刺专题卷12压轴题一、选择题（本大题共8个小题，每小题5分，共40分.在每小题给出的四个选项中，只有一个选项是符合题目要求的）1．（2023年·江苏中考真题）如图，△ABC中，AB=AC=2，∠B=30°，△ABC绕点A逆时针旋转α(0<α<120°)得到，与BC，AC分别交于点D，E.设，的面积为，则与的函数图象大致为()A．B．C．D．【答案】B【解析】连接B′C，作AH⊥B′C′，垂足为H， AB=AC，∠B=30°，∴∠C=∠B=30°， △ABC绕点A逆时针旋转α(0<α<120°)得到，∴AB′=AB=AC=AC′=2，∠AB′C′=∠C′=30°，∴AH=AC′=1，∴C′H=，∴B′C′=2C′H=2， AB′=AC，∴∠AB′C=∠ACB′， ∠AB′D=∠ACD=30°，∴∠AB′C-∠AB′D=∠ACB′-∠ACD，即∠DB′C=∠DCB′，∴B′D=CD， CD+DE=x，∴B′D+DE=x，即B′...