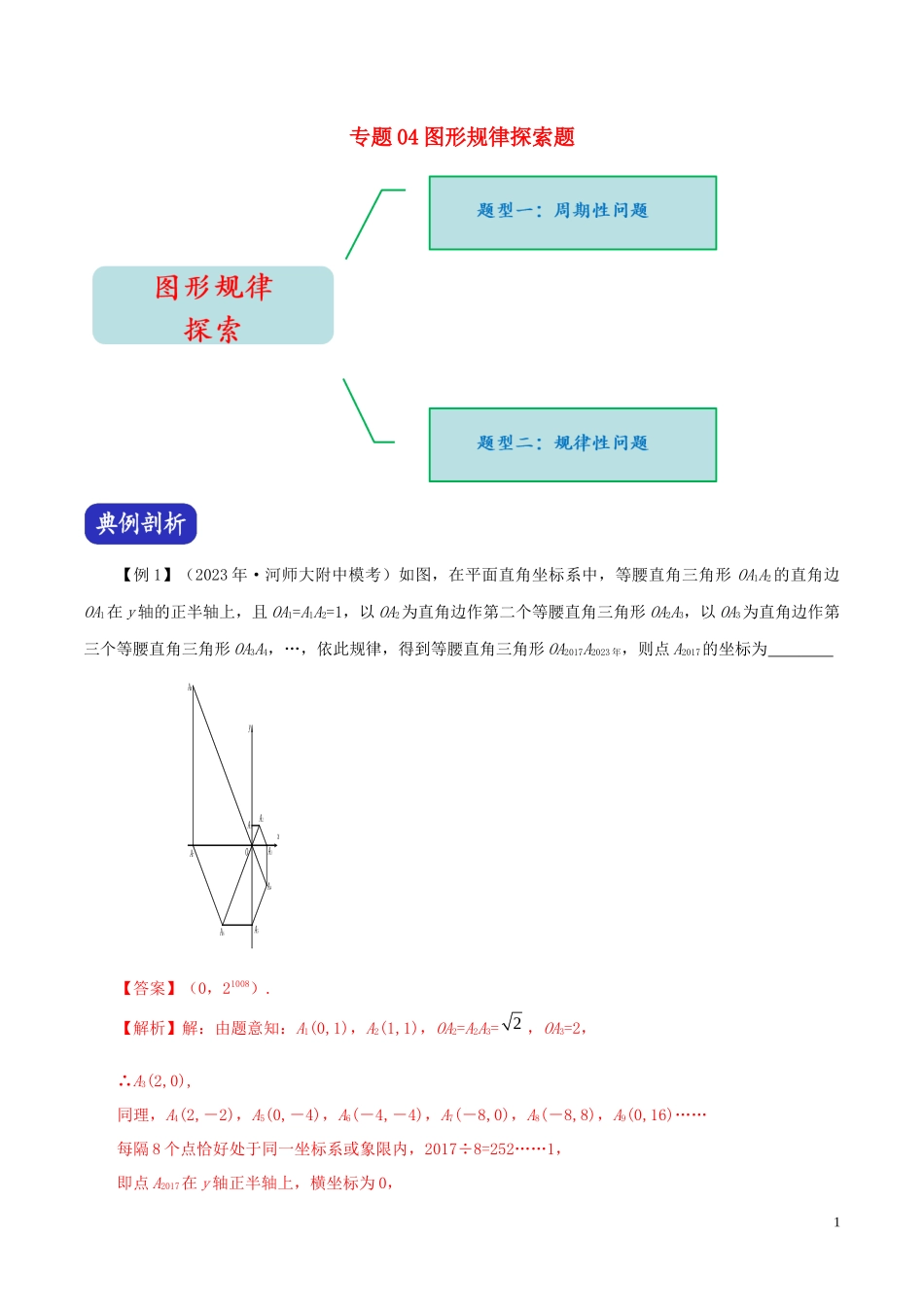
专题04图形规律探索题【例1】(2023年·河师大附中模考)如图,在平面直角坐标系中,等腰直角三角形OA1A2的直角边OA1在y轴的正半轴上,且OA1=A1A2=1,以OA2为直角边作第二个等腰直角三角形OA2A3,以OA3为直角边作第三个等腰直角三角形OA3A4,…,依此规律,得到等腰直角三角形OA2017A2023年,则点A2017的坐标为OxyA1A2A3A4A5A6A7A8【答案】(0,21008).【解析】解:由题意知:A1(0,1),A2(1,1),OA2=A2A3=,OA3=2,∴A3(2,0),同理,A4(2,-2),A5(0,-4),A6(-4,-4),A7(-8,0),A8(-8,8),A9(0,16)……每隔8个点恰好处于同一坐标系或象限内,2017÷8=252……1,即点A2017在y轴正半轴上,横坐标为0,21各点纵坐标的绝对值为:20,20,21,21,22,22,23,23,……2017÷2=1008……1,可得点A2017的纵坐标为:21008,...