2023学年中考数学压轴题冲刺提升专题02折叠与图形存在性含解析.docxVIP免费

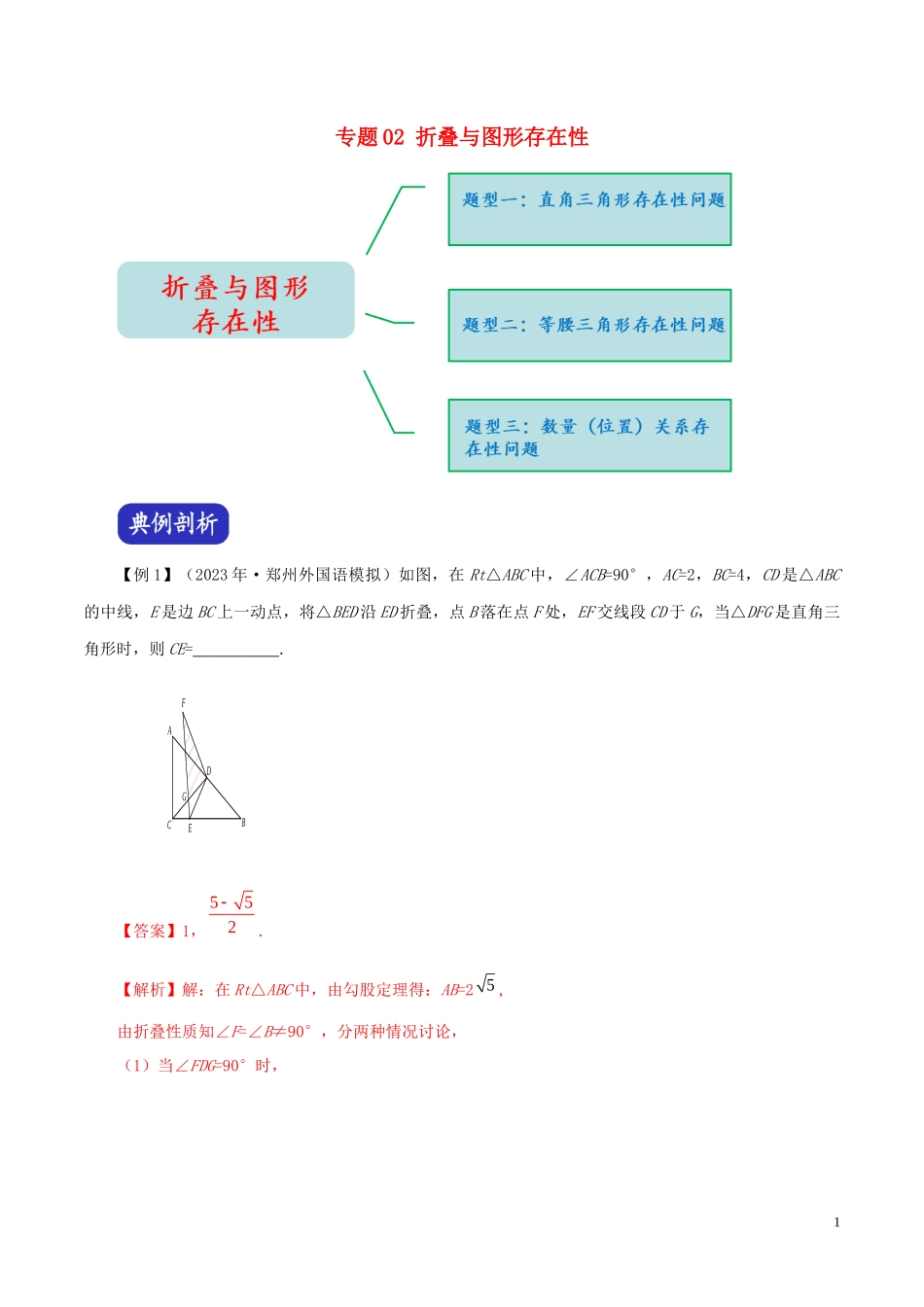
专题02折叠与图形存在性【例1】（2023年·郑州外国语模拟）如图，在Rt△ABC中，∠ACB=90°，AC=2，BC=4，CD是△ABC的中线，E是边BC上一动点，将△BED沿ED折叠，点B落在点F处，EF交线段CD于G，当△DFG是直角三角形时，则CE=.ACBDEFG【答案】1，.【解析】解：在Rt△ABC中，由勾股定理得：AB=2,由折叠性质知∠F=∠B≠90°，分两种情况讨论，（1）当∠FDG=90°时，55251ACBDEFG D是Rt△ABC斜边AB的中点，∴CD=BD=AD=，∴∠B=∠DCE=∠F， ∠DCE+∠GEC=∠F+∠FDG，∴∠GEC=90°，在Rt△DFG中，tan∠F=，∴DG=，∴CG=CD－DG=，在Rt△CEG中，CE=CG·cos∠GCE=×=1；（2）当∠FGD=90°时，ACBDEFG由（1）知∠B=∠F=∠DCB，由BD=DF=，∴DG=DF·sin∠F=×=1，5DGDF525252425552252∴CG=CD－DG=－1，∴CE=CG÷cos∠DCB=（...