2023学年中考数学压轴题冲刺提升专题05正确分析函数图象含解析.docxVIP免费

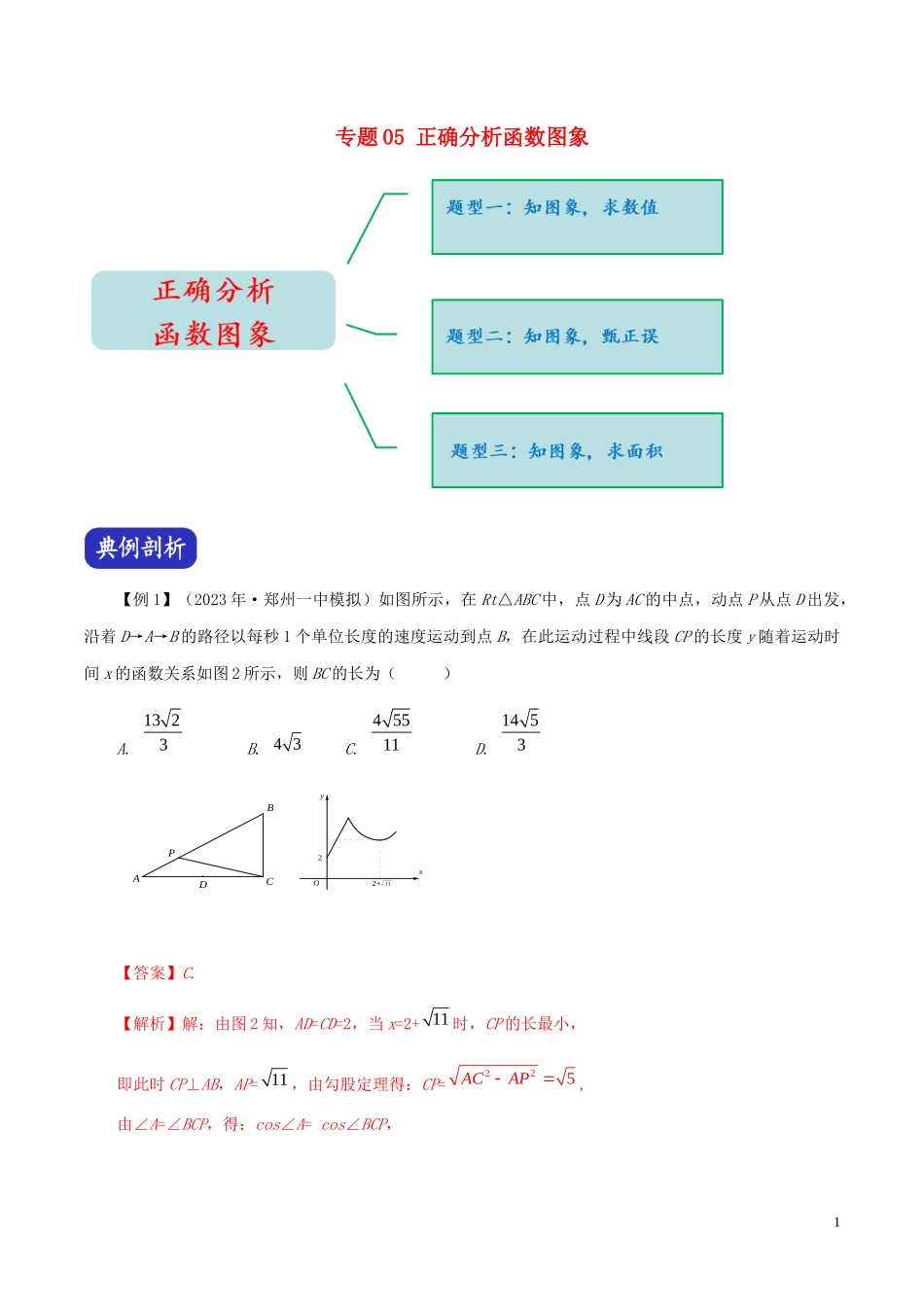
专题05正确分析函数图象【例1】（2023年·郑州一中模拟）如图所示，在Rt△ABC中，点D为AC的中点，动点P从点D出发，沿着D→A→B的路径以每秒1个单位长度的速度运动到点B，在此运动过程中线段CP的长度y随着运动时间x的函数关系如图2所示，则BC的长为（）A.B.C.D.ABCDPOxy22+11【答案】C.【解析】解：由图2知，AD=CD=2，当x=2+时，CP的长最小，即此时CP⊥AB，AP=，由勾股定理得：CP=,由∠A=∠BCP，得：cos∠A=cos∠BCP，1323434551114531111225ACAP1即：,解得：BC=,故答案为：C.【变式1-1】（2023年·郑州联考）如图所示，二次函数y＝ax2+bx+c（a≠0）的图象与x轴相交于点A，B，若其对称轴为直线x＝2，则OB﹣OA的值为．【答案】4．【解析】解：设A（x1，0），B（x2，0），x1、x2是方程ax2+bx+c＝0的两个根， 抛...