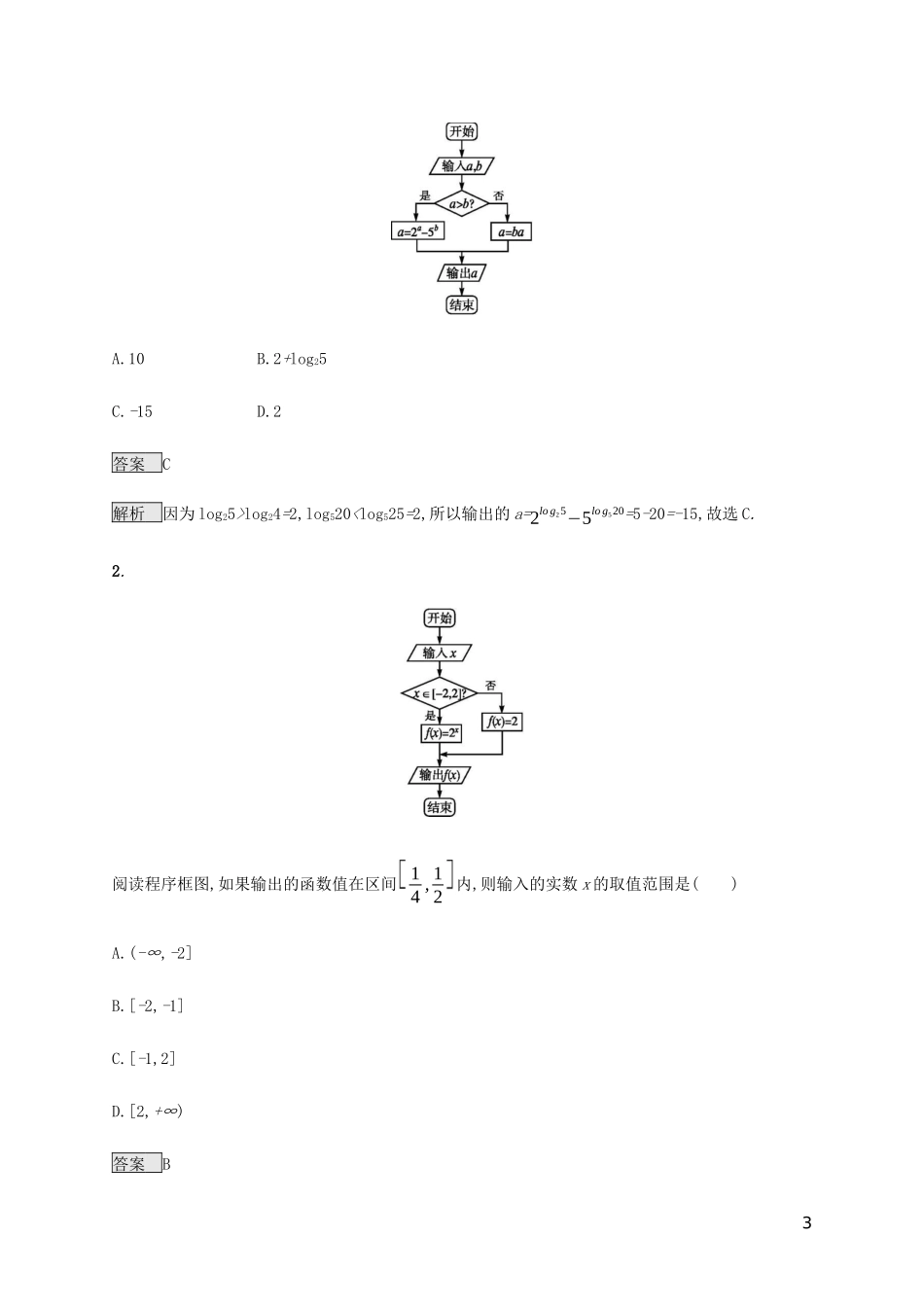
1.3程序框图命题角度1条件结构为主的结果输出型问题高考真题体验·对方向1.(2015全国Ⅱ·8)下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,18,则输出的a=()A.0B.2C.4D.14答案B解析由程序框图,得(14,18)→(14,4)→(10,4)→(6,4)→(2,4)→(2,2),则输出的a=2.2.(2013全国Ⅰ·5)执行下面的程序框图,如果输入的t∈[-1,3],则输出的s属于()1A.[-3,4]B.[-5,2]C.[-4,3]D.[-2,5]答案A解析若t∈[-1,1),则执行s=3t,故s∈[-3,3).若t∈[1,3],则执行s=4t-t2,其对称轴为t=2.故当t=2时,s取得最大值4.当t=1或3时,s取得最小值3,则s∈[3,4].综上可知,输出的s∈[-3,4].故选A.3.(2017江苏·4)下图是一个算法流程图.若输入x的值为116,则输出y的值是.答案-2解析由题意得y=...