2023学年高考数学大二轮复习能力升级练九空间几何体及三视图文2.docx

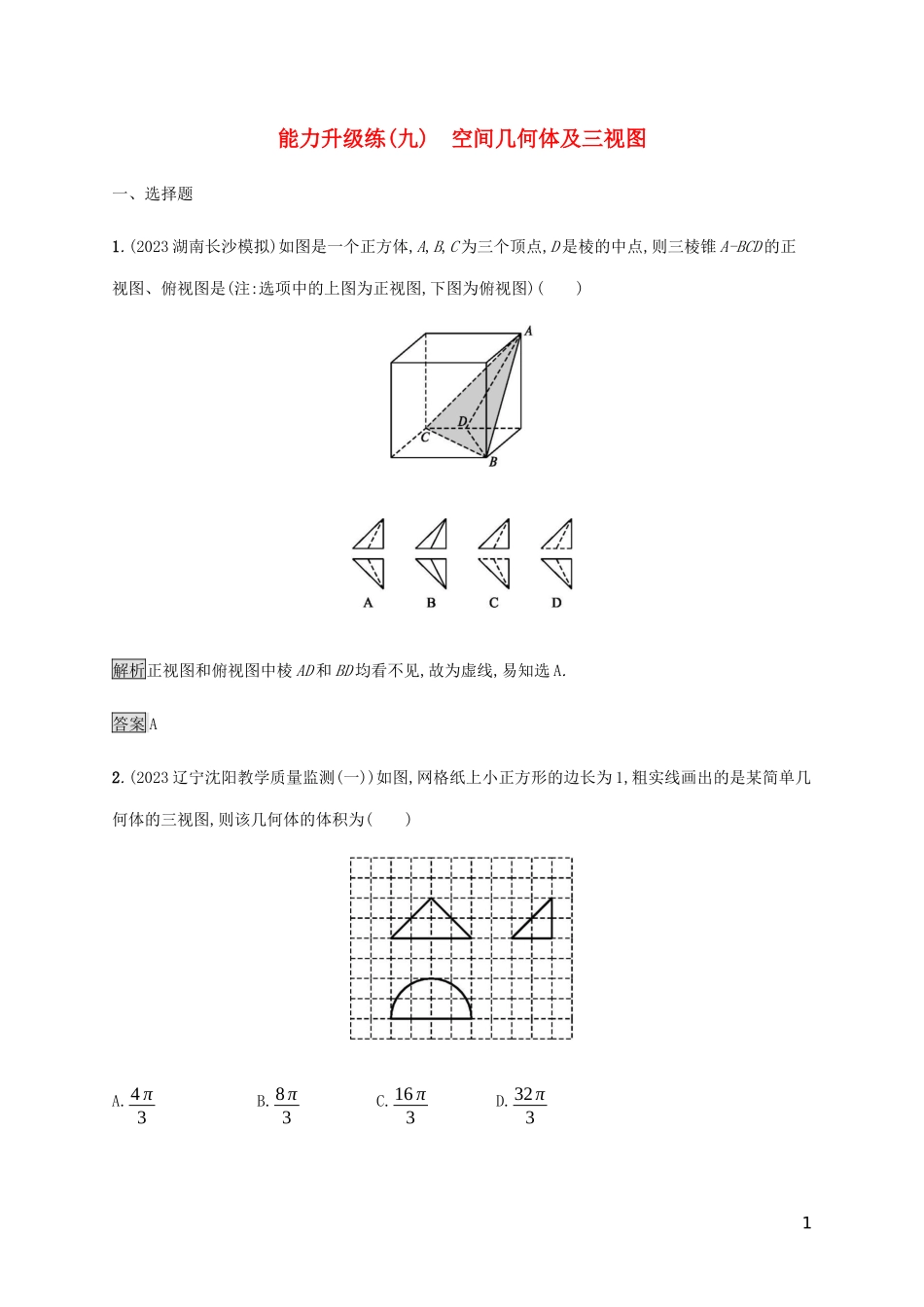
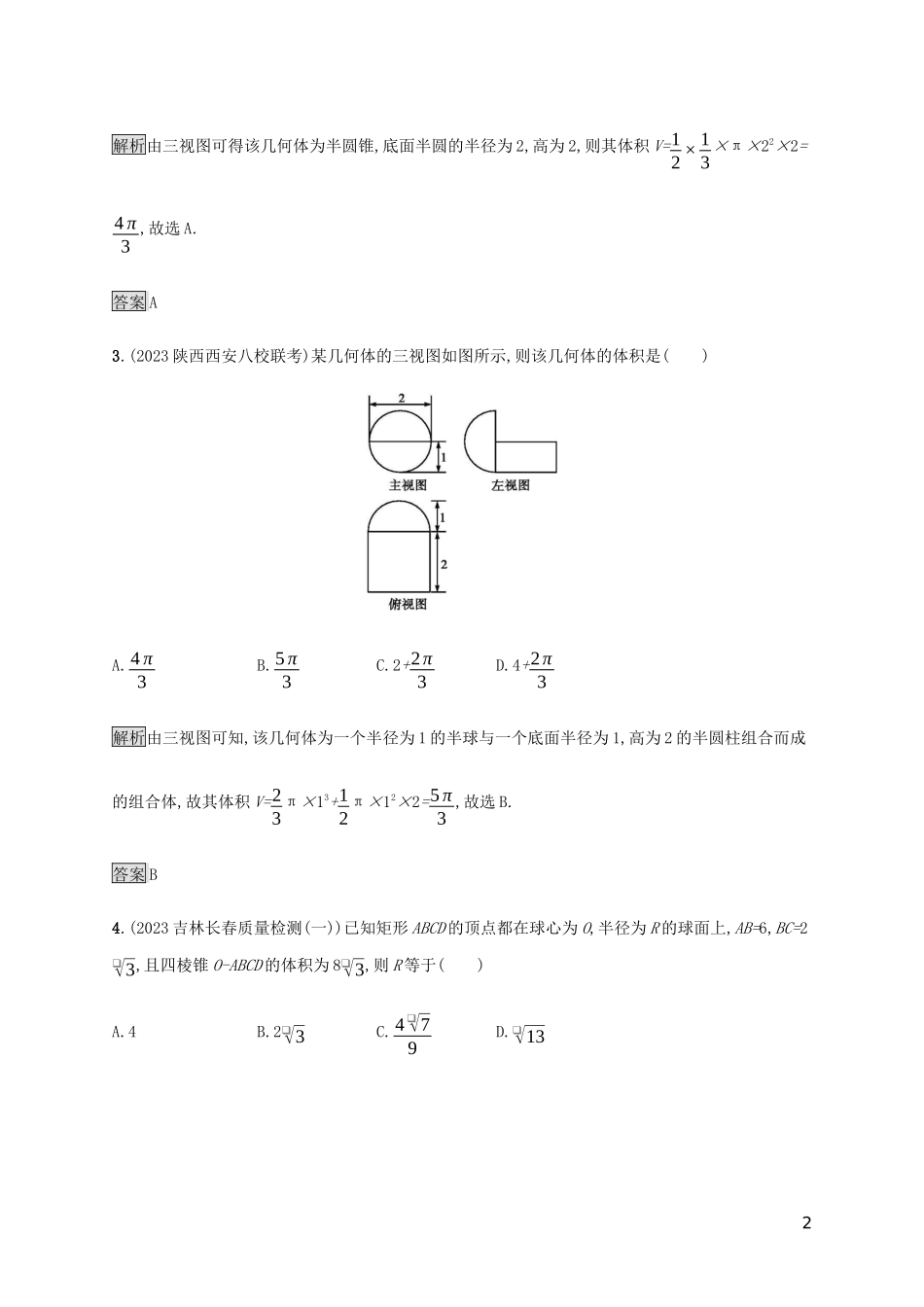
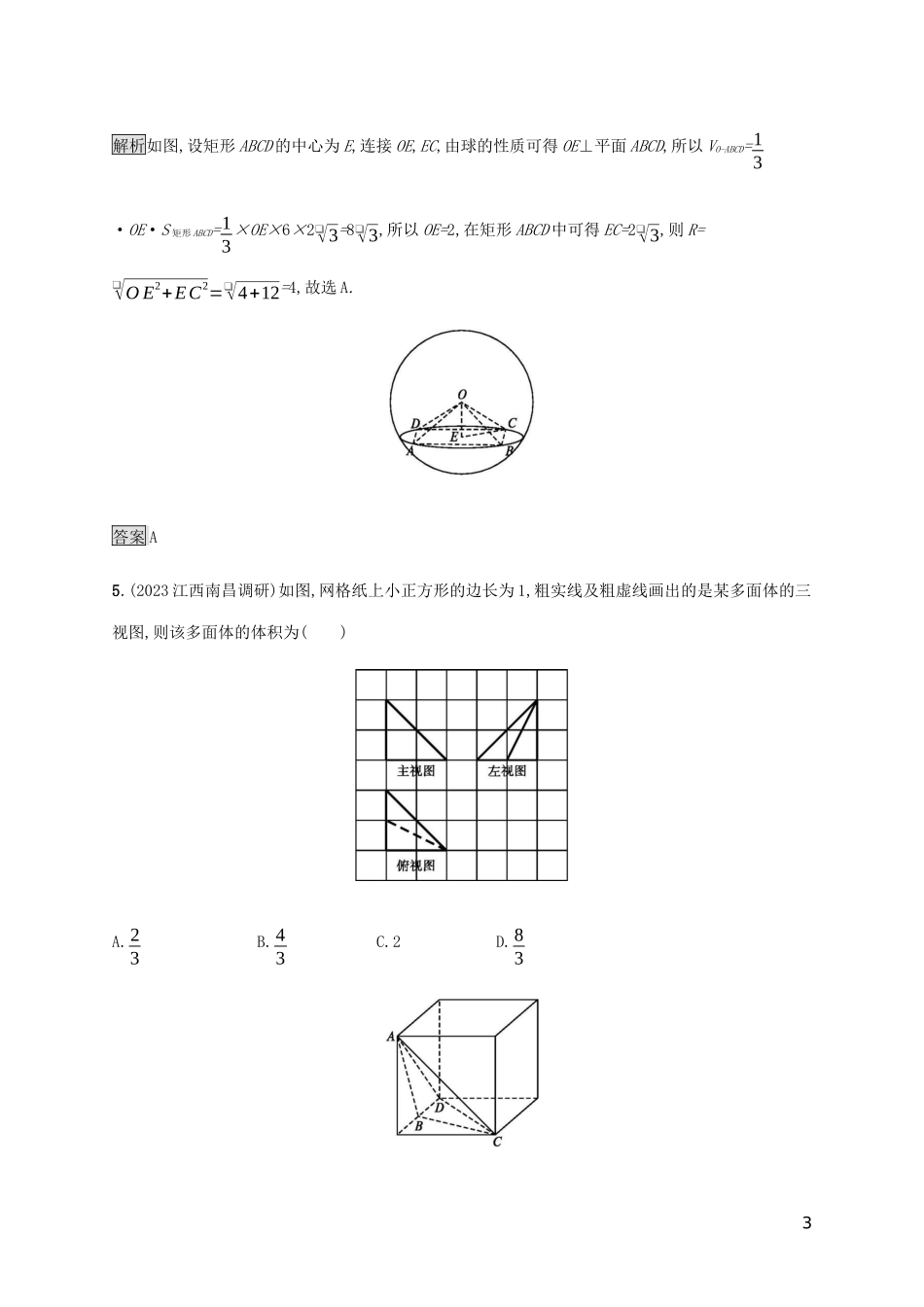
能力升级练(九)　空间几何体及三视图 一、选择题 1.(2023湖南长沙模拟)如图是一个正方体,A,B,C为三个顶点,D是棱的中点,则三棱锥A-BCD的正视图、俯视图是(注:选项中的上图为正视图,下图为俯视图)(　　) 解析正视图和俯视图中棱AD和BD均看不见,故为虚线,易知选A. 答案A 2.(2023辽宁沈阳教学质量监测(一))如图,网格纸上小正方形的边长为1,粗实线画出的是某简单几何体的三视图,则该几何体的体积为(　　) A.4π3 B.8π3 C.16π3 D.32π3 解析由三视图可得该几何体为半圆锥,底面半圆的半径为2,高为2,则其体积V=12×13×π×22×2=4π3,故选A. 答案A 3.(2023陕西西安八校联考)某几何体的三视图如图所示,则该几何体的体积是(　　) A.4π3 B.5π3 C.2+2π3 D.4+2π3 解析由三视图可知,该几何体为一个半径为1的半球与一个底面半径为1,高为2的半圆柱组合而成的组合体,故其体积V=23π×13+12π×12×2=5π3,故选B. 答案B 4.(2023吉林长春质量检测(一))已知矩形ABCD的顶点都在球心为O,半径为R的球面上,AB=6,BC=23,且四棱锥O-ABCD的体积为83,则R等于(　　) A.4 B.23 C.479 D.13 解析如图,设矩形ABCD的中心为E,连接OE,EC,由球的性质可得OE⊥平面ABCD,所以VO-ABCD=13·OE·S矩形ABCD=13×OE×6×23=83,所以OE=2,在矩形ABCD中可得EC=23,则R=OE2+EC2=4+12=4,故选A. 答案A 5.(2023江西南昌调研)如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体的体积为(　　) A.23 B.43 C.2 D.83 解析由三视图可知,该几何体为三棱锥,将其放在棱长为2的正方体中,如图中三棱锥A-BCD所示,故该几何体的体积V=13×12×1×2×2=23. 答案A 6.(2023辽宁五校协作体联考)如图所示,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是三棱锥的三视图,则此三棱锥的体积是(　　) A.8 B.16 C.24 D.48 解析由三视图还原三棱锥的直观图,如图中三棱锥P-ABC所示,且长方体的长、宽、高分别为6,2,4,△ABC是直角三角形,AB⊥BC,AB=2,BC=6,三棱锥P-ABC的高为4,故其体积为13×12×6×2×4=8,故选A. 答案A 7.将一个底面半径为1,高为2的圆锥形工件切割成一个圆柱体,能切割出的圆柱的最大体积为(　　) A.π27 B.8π27 C.π3 D.2π9 解析如图所示,设圆柱的半径为r,高为x,体积为V,由题意可得r1=2-x2,所以x=2-2r,所以圆柱的体积V=πr2(2-2r)=2π(r2-r3)(0<r<1),设V(r)=2π(r2-r3)(0<r<1),则V'(r)=2π(2r-3r2),由2π(2r-3r2)=0得r=23,所以圆柱的最大体积Vmax=2π232-233=8π27.故选B. 答案B 8.(2023福建福州模拟)如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的表面积为(　　) A.14 B.10+42 C.212+42 D.21+32+42 解析由三视图可知,该几何体为一个直三棱柱切去一个小三棱锥后剩余的几何体,如图所示.所以该多面体的表面积S=2×22-12×1×1+12×(22-12)+12×22+2×22+12×32×(2)2=21+32+42,故选D. 答案D 9.某几何体的三视图如图所示,则该几何体的体积的最大值为(　　) A.1 B.16 C.13 D.12 解析由三视图可知该几何体为三棱锥,设此三棱锥的高为x,则正视图中的长为6-x2,所以所求体积V=13×12×6-x2×1x=16(6-x2)x2≤16×6-x2+x22=12,当且仅当6-x2=x,即x=3时取等号,所以该几何体的体积的最大值为12. 答案D 二、填空题 10.(2023河南洛阳第一次联考)一个几何体的三视图如图所示,则该几何体的体积为　　　　　.  解析由题图可知该几何体是一个四棱锥,如图所示,其中PD⊥平面ABCD,底面ABCD是一个对角线长为2的正方形,底面积S=12×2×2=2,高h=1,则该几何体的体积V=13Sh=23. 答案23 11.(2023福建福州四校联考)已知某几何体的三视图如图所示,则该几何体的表面积为　　　　　.  解析在长、宽、高分别为3,33,33的长方体中,由几何体的三视图得几何体为如图所示的三棱锥C-BAP,其中底面BAP是∠BAP=90°的直角三角形,AB=3,AP=33,所以BP=6,又棱CB⊥平面BAP且CB=33,所以AC=6,所以该几何体的表面积是12×3×33+12×3×33+12×6×33+12×6×33=273. 答案273 12.(2023山东潍坊模拟)已知正四棱柱的顶点在同一个球面上,且球的表面积为12π,当正四棱柱的体积最大时,正四棱柱的高为　　　　　.  解析设正四棱柱的底面边长为a,高为h,球的半径为r,由题意知4πr2=12π,所以r2=3,又2a2+h2=(2r)2=12,所以a2=6-h22,所以正四棱柱的体积V=a2h=6-h22h,则V'=6-32h2,由V'>0,得0<h<2,由V'<0,得h>2,所以当h=2时,正四棱柱的体积最大,Vmax=8. 答案2 13.(2023江西南昌调研)已知三棱锥P-ABC的所有顶点都在球O的球面上,△ABC满足AB=22,∠ACB=90°,PA为球O的直径且PA=4,则点P到底面ABC的距离为　　　　　.  解析取AB的中点O1,连接OO1,如图,在△ABC中,AB=22,∠ACB=90°,所以△ABC所在小圆O1是以AB为直径的圆,所以O1A=2,且OO1⊥AO1,又球O的直径PA=4,所以OA=2,所以OO1=OA2-O1A2=2,且OO1⊥底面ABC,所以点P到平面ABC的距离为2OO1=22. 答案22 三、解答题 14.如图所示,正四棱台的高是17 cm,两底面边长分别为4 cm和16 cm,求棱台的侧棱长和斜高. 解设棱台两底面的中心分别为O'和O,B'C',BC的中点分别为E',E,连接O'B',O'E',O'O,OE,OB,EE',则四边形O'E'EO,OBB'O'均为直角梯形. 在正方形ABCD中,BC=16cm, 则OB=82cm,OE=8cm, 在正方形A'B'C'D'中,B'C'=4cm, 则O'B'=22cm,O'E'=2cm, 在直角梯形O'OBB'中, BB'=OO'2+(OB-O'B')2=19(cm); 在直角梯形O'OEE'中, EE'=OO'2+(OE-O'E')2=513(cm). 所以这个棱台的侧棱长为19cm,斜高为513cm. 15.现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P-A1B1C1D1,下部的形状是正四棱柱ABCD-A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍,若AB=6 m,PO1=2 m,则仓库的容积是多少? 解由PO1=2m,知O1O=4PO1=8m. 因为A1B1=AB=6m,所以正四棱锥P-A1B1C1D1的体积V锥=13·A1B12·PO1=13×62×2=24(m3); 正四棱柱ABCD-A1B1C1D1的体积 V柱=AB2·O1O=62×8=288(m3), 所以仓库的容积V=V锥+V柱=24+288=312(m3). 故仓库的容积是312m3. 10