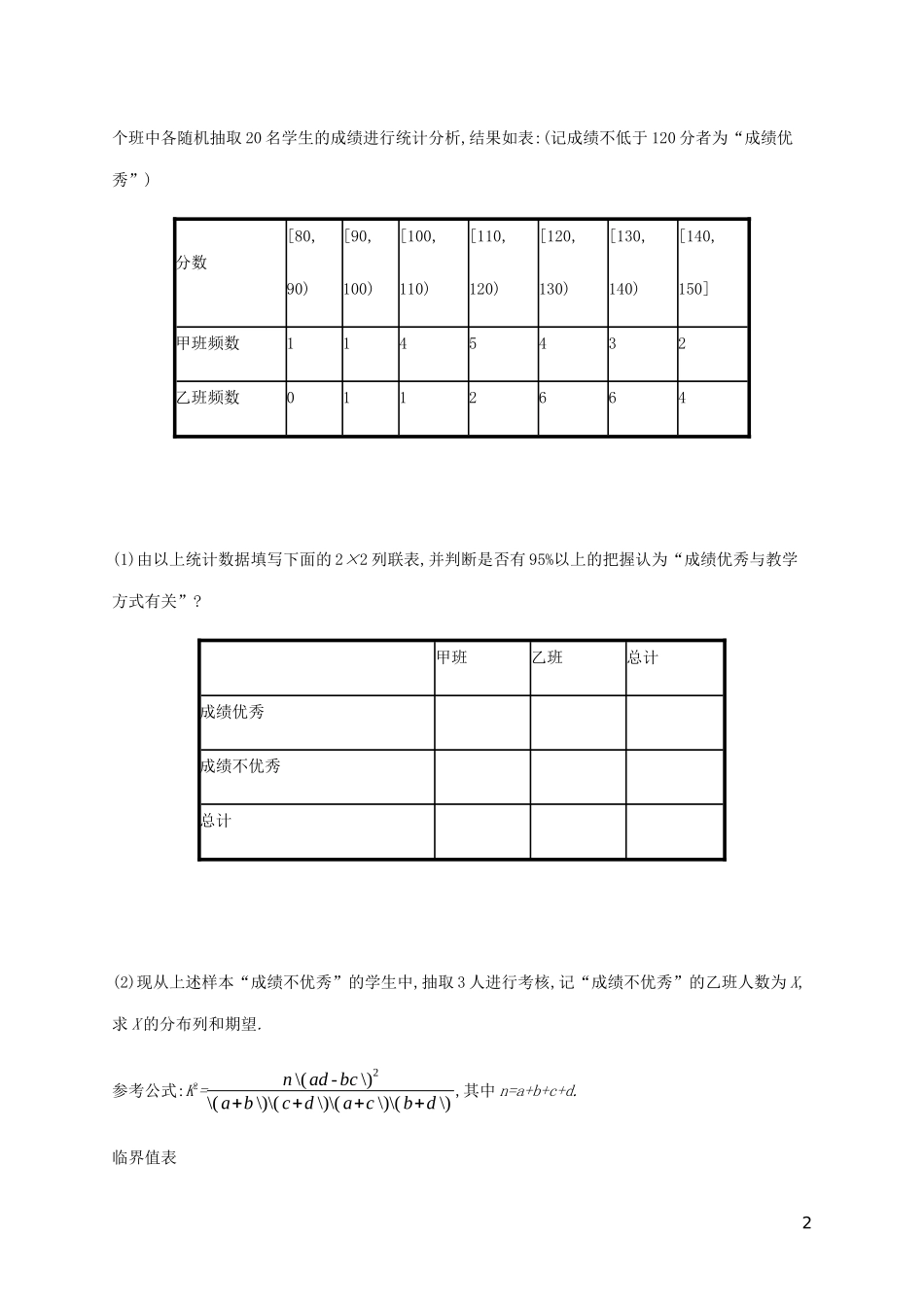
大题专项练(四)概率与统计A组基础通关1.袋子里有除颜色外完全相同的3只红球和4只黑球,今从袋子里随机取球.(1)若有放回地取3次,每次取一个球,求取出2个红球1个黑球的概率;(2)若无放回地取3次,每次取一个球,若取出每只红球得2分,取出每只黑球得1分,求得分ξ的分布列和数学期望.解(1)从袋子里有放回地取3次球,相当于做了3次独立重复试验,每次试验取出红球的概率为37,取出黑球的概率为47,设事件A=“取出2个红球1个黑球”,则P(A)=C32(37)2(47)=3×949×47=108343.(2)ξ的取值可以是3,4,5,6.P(ξ=3)=C30C43C73=435,P(ξ=4)=C31C42C73=1835,P(ξ=5)=C32C41C73=1235,P(ξ=6)=C33C40C73=135.ξ3456P43518351235135从而得分ξ的数学期望Eξ=3×435+4×1835+5×1235+6×135=307.2.为了适应高考改革,某中学推行“创新课堂”教...