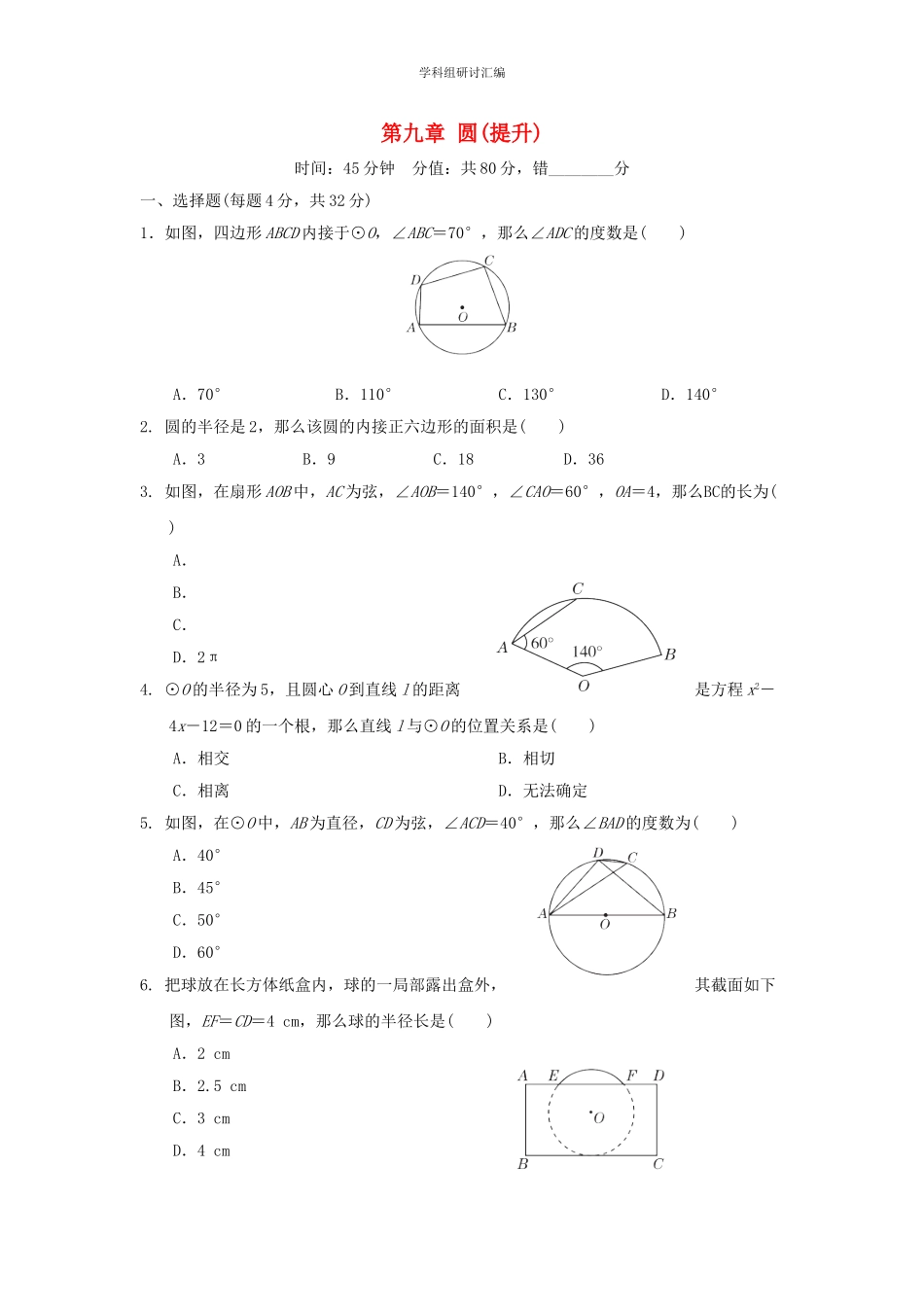
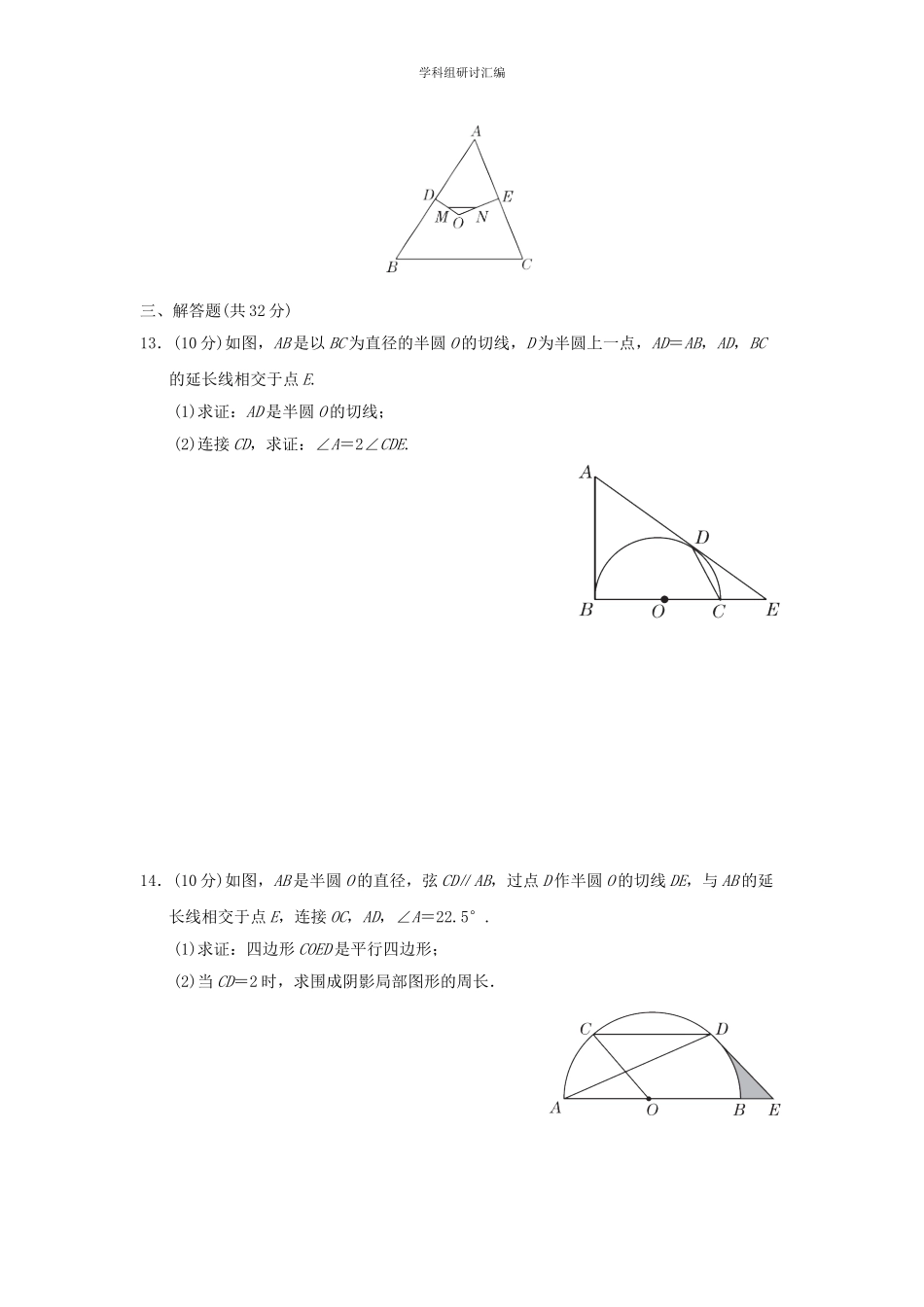
学科组研讨汇编第九章圆(提升)时间:45分钟分值:共80分,错________分一、选择题(每题4分,共32分)1.如图,四边形ABCD内接于⊙O,∠ABC=70°,那么∠ADC的度数是()A.70°B.110°C.130°D.140°2.圆的半径是2,那么该圆的内接正六边形的面积是()A.3B.9C.18D.363.如图,在扇形AOB中,AC为弦,∠AOB=140°,∠CAO=60°,OA=4,那么BC的长为()A.B.C.D.2π4.⊙O的半径为5,且圆心O到直线l的距离是方程x2-4x-12=0的一个根,那么直线l与⊙O的位置关系是()A.相交B.相切C.相离D.无法确定5.如图,在⊙O中,AB为直径,CD为弦,∠ACD=40°,那么∠BAD的度数为()A.40°B.45°C.50°D.60°6.把球放在长方体纸盒内,球的一局部露出盒外,其截面如下图,EF=CD=4cm,那么球的半径长是()A.2cmB.2.5cmC.3cmD.4cm学科组研讨汇编7.如图,AB是⊙O的弦,点C是优弧AB上的动点(C不与A,B重合),CH⊥AB,垂足为H,点M是BC的中点.假设⊙O的半径是3,那么MH长的最大值是()A.3B.4C.5D.68.如图,弦AB与弦CD交于点P,且P为AB的中点,延长AC,DB交于点E,假设AC=2,BD=3,那么EC+EB=()A.9B.3+4C.10D.6二、填空题(每题4分,共16分)9.如图,点A,B,C在⊙O上,分别连接AB,BC,OC.假设AB=BC,∠B=40°,那么∠OCB=________.10.圆锥的底面圆的半径是3,其母线长是9,那么圆锥侧面展开图的扇形的圆心角度数是________°.11.如图,在▱ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD长为半径画弧交AB于点E,连接CE,那么阴影局部的面积是________.(结果保存π)12.如图,点O是△ABC的外心,OD⊥AB,OE⊥AC,垂足分别为D,E,点M,N分别是OD,OE的中点,连接MN,假设MN=2,那么BC=________.学科组研讨汇编三、解答题(共32分)13.(10分)如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.(1)求证:AD是半圆O的切线;(2)连接CD,求证:∠A=2∠CDE.14.(10分)如图,AB是半圆O的直径,弦CD∥AB,过点D作半圆O的切线DE,与AB的延长线相交于点E,连接OC,AD,∠A=22.5°.(1)求证:四边形COED是平行四边形;(2)当CD=2时,求围成阴影局部图形的周长.学科组研讨汇编12.(实验中学2023中考模拟〕(12分)如图,AB与⊙O相切于点A,P为OB上一点,且BP=BA,连接AP并延长交⊙O于点C,连接OC.(1)求证:OC⊥OB;(2)假设⊙O的半径为4,AB=3,求AP的长.学科组研讨汇编参考答案一、1.B2.(衡水中学2023...