北京市2023年中考数学真题模拟题汇编专题10图形的性质之选择题含解析.docVIP免费

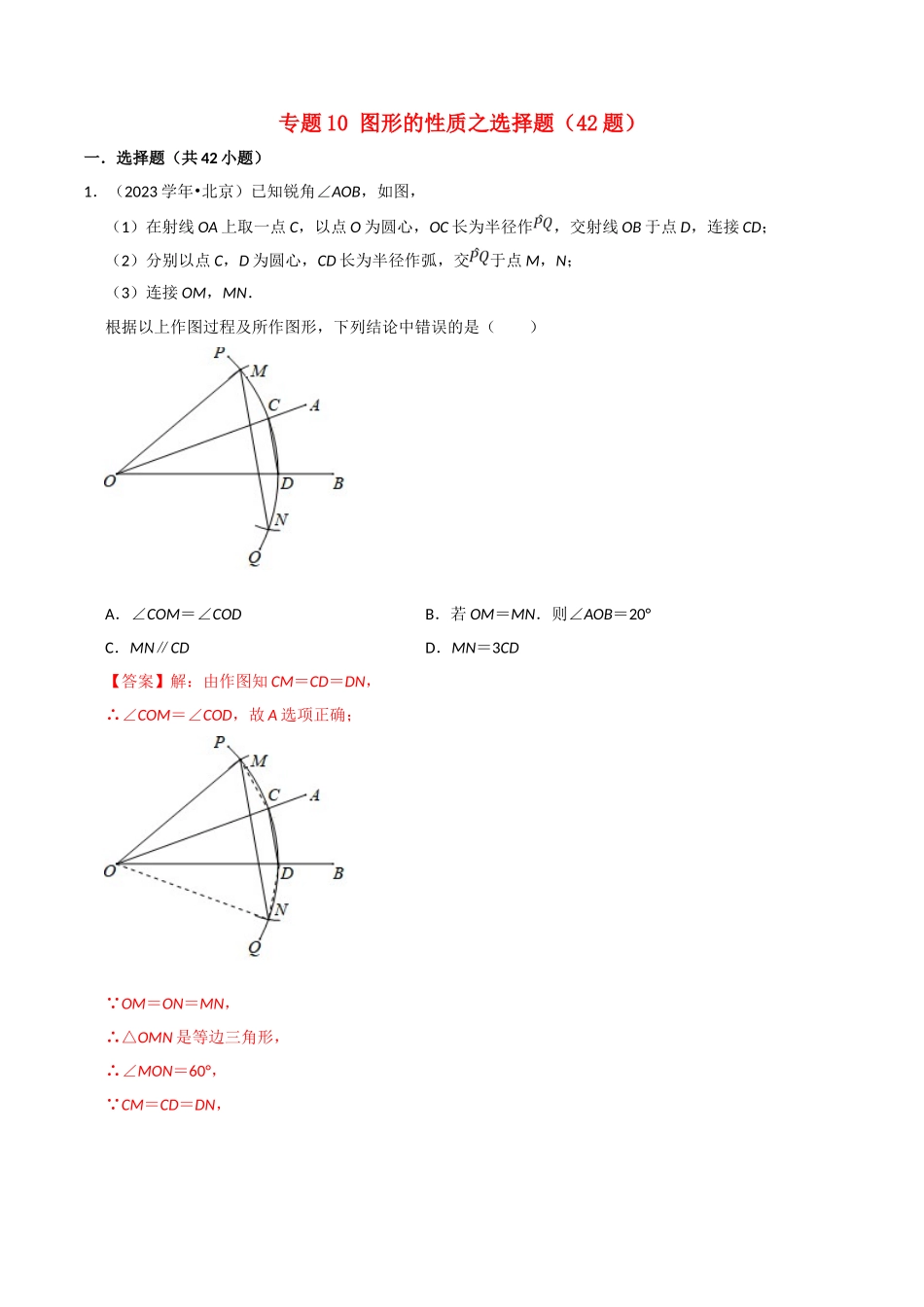
专题10图形的性质之选择题（42题）一．选择题（共42小题）1．（2023学年•北京）已知锐角∠AOB，如图，（1）在射线OA上取一点C，以点O为圆心，OC长为半径作，交射线OB于点D，连接CD；（2）分别以点C，D为圆心，CD长为半径作弧，交于点M，N；（3）连接OM，MN．根据以上作图过程及所作图形，下列结论中错误的是（）A．∠COM＝∠CODB．若OM＝MN．则∠AOB＝20°C．MN∥CDD．MN＝3CD【答案】解：由作图知CM＝CD＝DN，∴∠COM＝∠COD，故A选项正确； OM＝ON＝MN，∴△OMN是等边三角形，∴∠MON＝60°， CM＝CD＝DN，∴∠MOA＝∠AOB＝∠BON∠MON＝20°，故B选项正确；设∠MOA＝∠AOB＝∠BON＝α，则∠OCD＝∠OCM，∴∠MCD＝180°﹣α，又 ∠CMN∠OCN＝α，∴∠MCD+∠CMN＝180°，∴MN∥CD，故C选项正确； MC+CD+DN＞M...