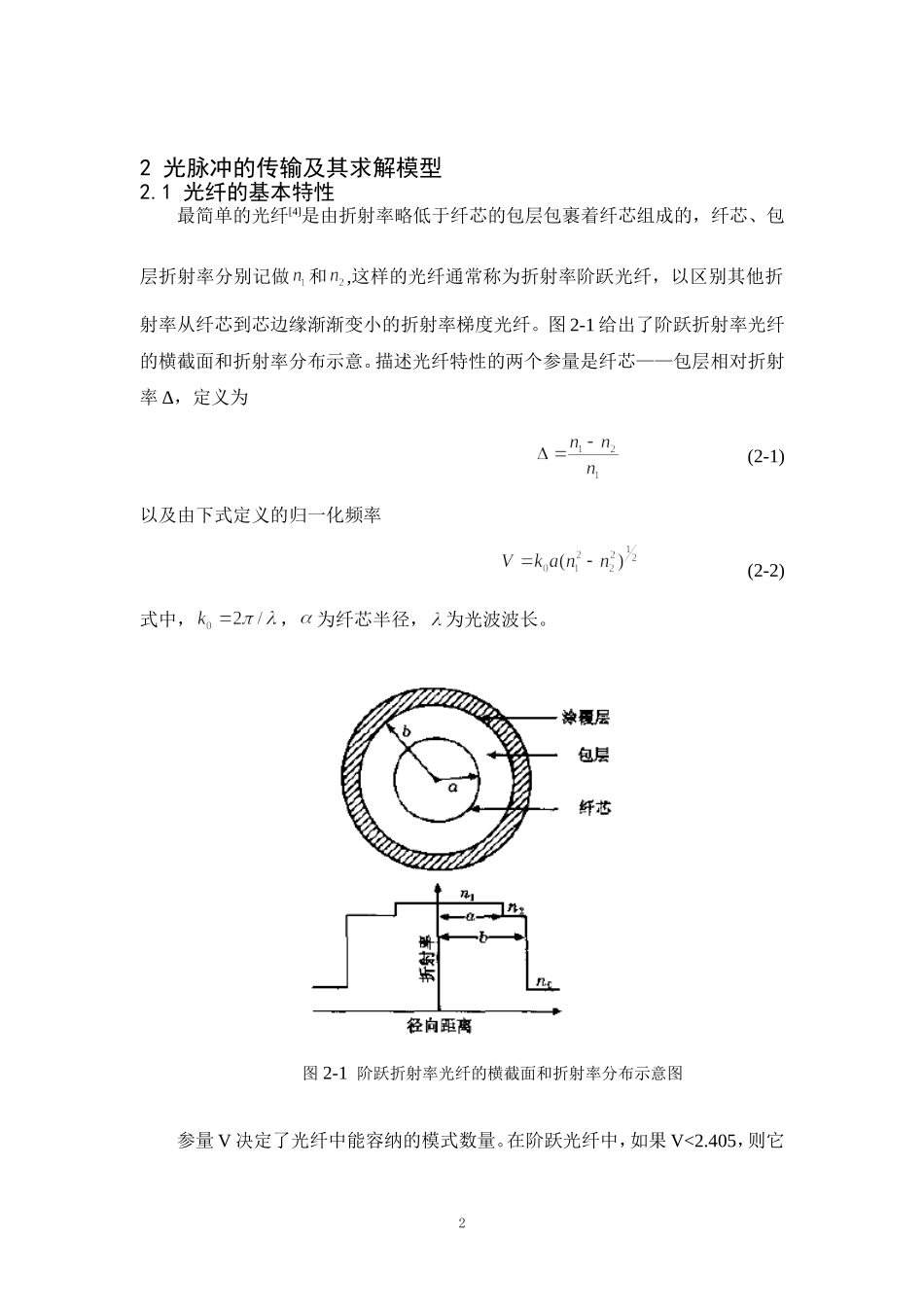
1绪论1.1课题研究背景与意义超连续(SC)谱指的是强短光脉冲在通过非线性介质(如光纤)时所形成的极大展宽光谱。超连续谱的产生是指当一束强高峰值功率的光脉冲通过光纤后,透射谱中出现许多新的频率成分,使光谱的宽度展宽远远大于入射脉冲的谱宽。该现象的产生是由于光纤中的自相位调制(SPM),交叉相位调制(XPM)等非线性效应和色散以及啁啾等共同作用的结果,受激拉曼散射(SRS)也会引起光谱展宽。同其他用于光纤通信的超短脉冲光源相比,超连续谱具有连续宽带谱、稳定可靠、简单廉价等诸多优点,将在未来的Tbit/s波分复用/光时分复用(WDM/OTDM)系统中扮演重要角色。利用光纤中的超连续(SC)谱展宽技术,能够在很宽的光谱范围内同时获得多个高重复率、多波长超短脉冲,是一种有效的超短脉冲光源产生方法。而超短脉冲光源是非线性光学、信息光电子超快光谱和多光子显微镜等诸多应用领域的关键器件,具有广阔的应用前景[1]。近年来,光纤中的光谱超连续展宽技术已经成为当前热门的研究课题。SC谱光源以其优越的性能在光谱检测、生物医学、高精密光学频率测量及波分复用光通信系统等方面有着重要的作用,主要有以下几个方面:波形和群速度测量、超高速WDM系统光源、实现无抽运的自频移、全光解复用。同时,利用SC谱光源还可以实现高分辨率的DCT。此外,SC谱在超短脉冲压缩、激光光谱学和传感技术方面也有大的应用潜力[2]。1.2本文的主要内容以上是关于本课题的研究背景及意义,本文主要利用MATLAB进行模拟、分析研究双曲正割脉冲[3]在一段级联光纤中传输的光谱展宽特性。最后得到级联光纤中双曲正割脉冲展宽的规律。全文结构如下:第一章主要介绍课题背景、意义以及本文的内容;第二章主要讲脉冲在光纤中传输的基本特性,包括损耗、色散效应、非线性效应等,然后介绍了光纤中的非线性传输方程——非线性薛定谔方程及其求解方法;第三章通过MATLAB进行模拟,分析在级联光纤中双曲正割脉冲光谱展宽特性,得出结论;第四章综合前文对全文进行总结。12光脉冲的传输及其求解模型2.1光纤的基本特性最简单的光纤[4]是由折射率略低于纤芯的包层包裹着纤芯组成的,纤芯、包层折射率分别记做和,这样的光纤通常称为折射率阶跃光纤,以区别其他折射率从纤芯到芯边缘渐渐变小的折射率梯度光纤。图2-1给出了阶跃折射率光纤的横截面和折射率分布示意。描述光纤特性的两个参量是纤芯——包层相对折射率Δ,定义为(2-1)以及由下式定义的归一化频率(2-2)式中,,为纤芯半...