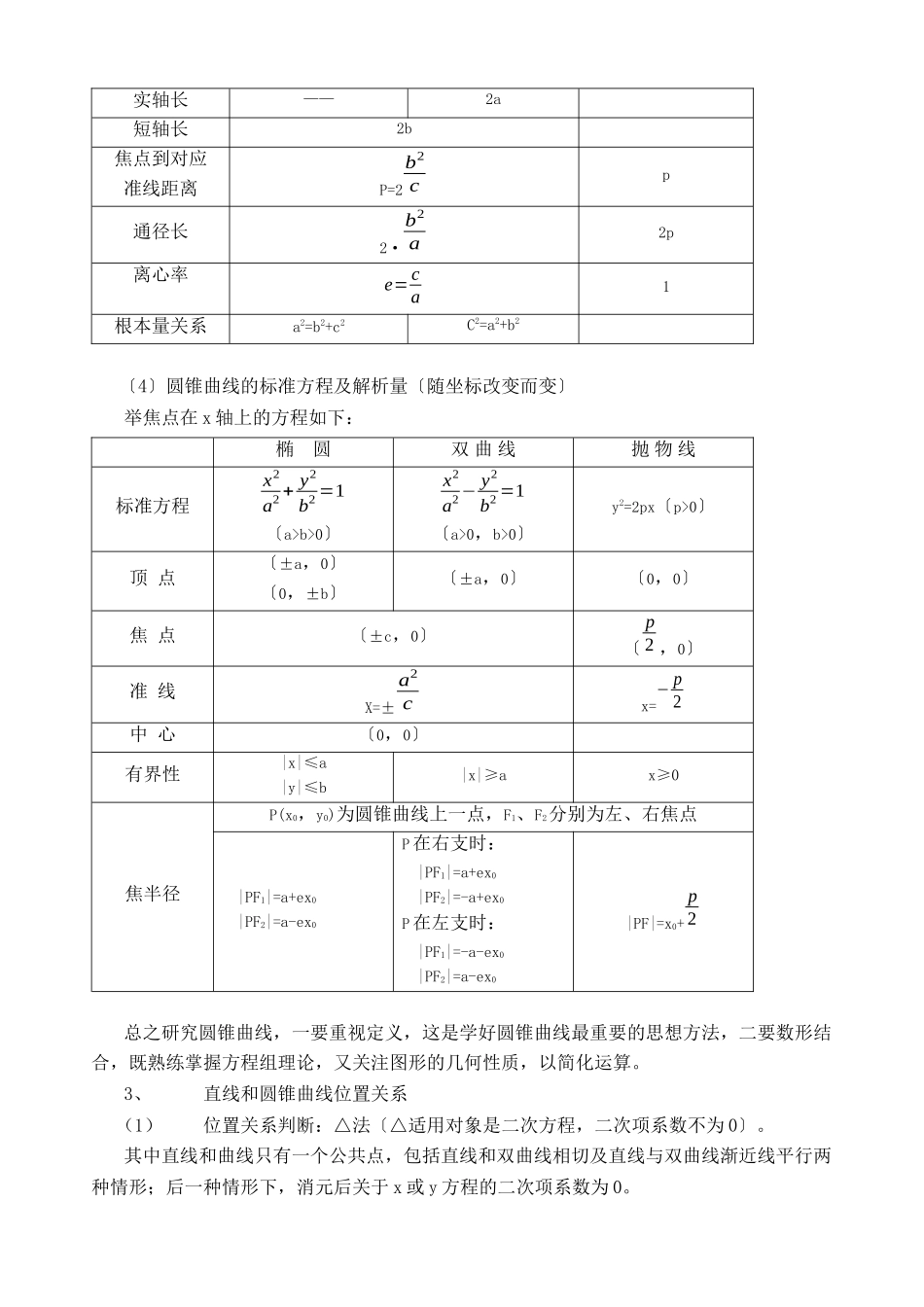
2023年高三一轮复习讲座八----圆锥曲线方程主讲教师:王思俭〔苏州中学〕二、复习要求1、三种圆锥曲线:椭圆、双曲线、抛物线的定义、标准方程、几何性质等。2、直线和圆锥曲线位置关系。3、求轨迹方程的常规方法。三、学习指导1、上一章已经复习过解析几何的根本问题之一:如何求曲线〔点的轨迹〕方程。它一般分为两类基此题型:一是轨迹类型求其方程,常用待定系数法,如求直线及圆的方程就是典型例题;二是未知轨迹类型,此时除了用代入法、交轨法、参数法等求轨迹的方法外,通常设法利用轨迹的定义解题,化归为求轨迹类型的轨迹方程。因此在求动点轨迹方程的过程中,一是寻找与动点坐标有关的方程〔等量关系〕,侧重于数的运算,一是寻找与动点有关的几何条件,侧重于形,重视图形几何性质的运用。在根本轨迹中,除了直线、圆外,还有三种圆锥曲线:椭圆、双曲线、抛物线。2、三种圆锥曲线的研究〔1〕统一定义,三种圆锥曲线均可看成是这样的点集:{P||PF|d=e,e>0},其中F为定点,d为P到定直线的距离,F∉,如图。因为三者有统一定义,所以,它们的一些性质,研究它们的一些方法都具有规律性。当01时,点P轨迹是双曲线;当e=1时,点P轨迹是抛物线。〔2〕椭圆及双曲线几何定义:椭圆:{P||PF1|+|PF2|=2a,2a>|F1F2|>0,F1、F2为定点},双曲线{P|||PF1|-|PF2||=2a,|F1F2|>2a>0,F1,F2为定点}。〔3〕圆锥曲线的几何性质:几何性质是圆锥曲线内在的,固有的性质,不因为位置的改变而改变。①定性:焦点在与准线垂直的对称轴上椭圆及双曲线中:中心为两焦点中点,两准线关于中心对称;椭圆及双曲线关于长轴、短轴或实轴、虚轴成轴对称,关于中心成中心对称。②定量:椭圆双曲线抛物线焦距2c长轴长2a——实轴长——2a短轴长2b焦点到对应准线距离P=2b2cp通径长2·b2a2p离心率e=ca1根本量关系a2=b2+c2C2=a2+b2〔4〕圆锥曲线的标准方程及解析量〔随坐标改变而变〕举焦点在x轴上的方程如下:椭圆双曲线抛物线标准方程x2a2+y2b2=1〔a>b>0〕x2a2−y2b2=1〔a>0,b>0〕y2=2px〔p>0〕顶点〔±a,0〕〔0,±b〕〔±a,0〕〔0,0〕焦点〔±c,0〕〔p2,0〕准线X=±a2cx=−p2中心〔0,0〕有界性|x|≤a|y|≤b|x|≥ax≥0焦半径P(x0,y0)为圆锥曲线上一点,F1、F2分别为左、右焦点|PF1|=a+ex0|PF2|=a-ex0P在右支时:|PF1|=a+ex0|PF2|=-a+ex0P在左支时:|PF1|=-a-ex0|PF2|=a-ex0|PF|=x0+p2总之研究圆锥曲线,一要重视定义,这是学好...